Fracciones

Definición
Una fracción es un número, que se obtiene de dividir un entero en partes iguales. Por ejemplo cuando decimos una cuarta parte de la torta, estamos dividiendo la torta en cuatro partes y consideramos una de ellas.
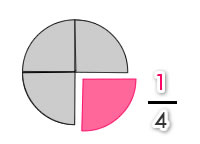
Elementos de una Fracción
Una fracción se representa matemáticamente por números que están escritos uno sobre otro y que se hallan separados por una línea recta horizontal llamada raya fraccionaria.
La fracción está formada por dos términos: el numerador y el denominador.
El numerador es el número que está sobre la raya fraccionaria; es el número de partes que se considera de la unidad o total.
El denominador es el que está bajo la raya fraccionaria; es el número de partes iguales en que se ha dividido la unidad o total.
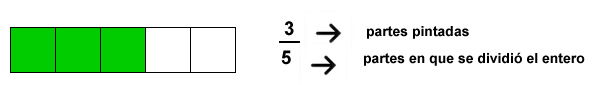
Números Naturales y Fracciones
Para negociar y ordenar cosas, el hombre tuvo la necesidad de representar las cantidades de lo que tenía para saber con qué contaba exactamente. De ahí surgió la necesidad de crear símbolos que representaran esas cantidades.
Los números naturales son aquellos símbolos que nos permiten representar la cantidad de elementos que tiene un conjunto.

Debido a la importancia de este conjunto de números se creó un símbolo especial para identificarlo, usaremos la letra ℕ para representar el conjunto de los números naturales; así, cuando veas esta ℕ en un libro de matemáticas, o en alguna clase, sabrás a qué se refiere.
¿Te has preguntado cuál es el último número natural? No hay, sencillamente no existe un número natural que sea más grande que todos los demás, cada vez que pienses en uno, podrás encontrar muchos que sean mayores que él. Como no terminan nunca, decimos que ℕ es un conjunto infinito.
Los números naturales poseen propiedades únicas que los diferencian de los demás conjuntos numéricos.
Operaciones en el conjunto de los números naturales

Los números naturales son aquellos que nos permiten contar los elementos de un determinado conjunto. Gracias a esto, cuando realizamos operaciones con ellos, los resultados pueden ser o no números naturales.
Lectura de Fracciones
Todas las fracciones reciben un nombre específico, se pueden leer como tal, de acuerdo al numerador y denominador que tengan.
El número que está en el numerador se lee igual, no así el denominador. Cuando el denominador va de 2 a 10, tiene un nombre específico (si es 2 es «medios», si es 3 es «tercios», si es 4 es «cuartos», si es 5 es «quintos», si es 6 es «sextos», si es 7 es «séptimos», si es 8 es «octavos», si es 9 es «novenos», si es 10 es «décimos»), sin embargo, cuando es mayor que 10 se le agrega al número la terminación «avos».
Las Fracciones en la Recta Numérica
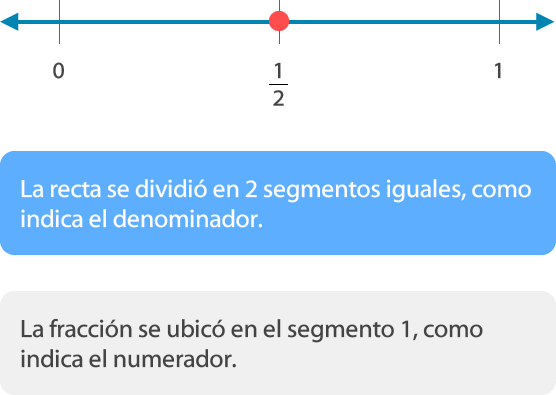
Para ubicar fracciones en la recta numérica se divide la unidad (entero) en segmentos iguales, como indica el denominador, y se ubica la facción según indica el numerador.
Ejemplo de fracciones unitarias (con numerador 1) en la recta numérica:
a). Ubicar la fracción 1/2
b). Ubicar la fracción 1/5

Como puedes observar las fracciones unitarias se ubican en el primer segmento de la recta numérica.
¿Cómo ubicar fracciones que no son unitarias?
Para ubicar fracciones que no son unitarias en la recta numérica se realiza el mismo procedimiento anterior, es decir, se divide el entero en partes iguales según lo que indique el denominador de la fracción. Luego, se ubica la fracción en el segmento que está señalado en el numerador.
Por ejemplo:
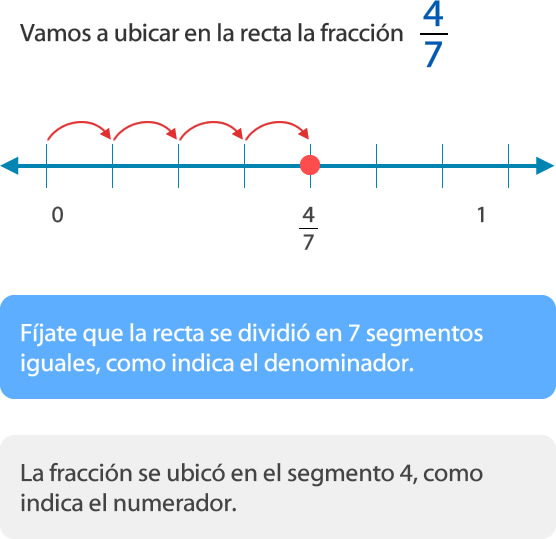
Recuerda que en la recta numérica el mayor de dos números es el que está más a la derecha.
Fracciones Equivalentes
Fíjate en la siguiente imagen:
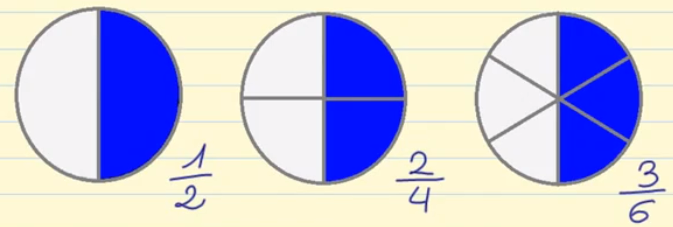
La primera figura está dividida en dos partes y hemos coloreado una de ellas. Por lo tanto, su fracción será 1/2.
La segunda figura la hemos dividido en 4 partes y hemos coloreado dos. Por lo tanto su fracción será 2/4.
Y la tercera figura la hemos dividido en 6 partes y hemos coloreado 3, por lo que su fracción será 3/6.
Si te fijas la parte coloreada en todas las figuras es la misma aunque las fracciones son diferentes: las tres fracciones dan el mismo resultado, son equivalentes.
Suma y Resta de Fracciones con Denominadores Comunes
Al tener el mismo denominador en las fracciones que vamos a sumar o restar, dejamos el mismo denominador y sumamos o restamos el numerador.
Vamos a ver un ejemplo. Si sumamos 7/10 y 10/10, dejamos 10 como denominador de la fracción resultante y sumamos los numeradores, 7 + 10 = 17.
El resultado de la fracción sería 17/10.
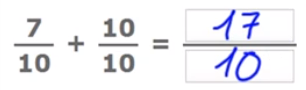
Suma y Resta de Fracciones con Denominadores Diferentes


Para calcular la suma o resta de este tipo de fracciones tendremos que multiplicar los denominadores para hallar el denominador de la fracción resultante, y para conseguir el numerador tendríamos que multiplicar el numerador de una de las fracciones por el denominador de la otra y viceversa, y posteriormente, sumar o restar el resultado, dependiendo del tipo de operación que tengamos que realizar.
Vamos a poner un ejemplo. Sumemos 11/10 + 2/3.
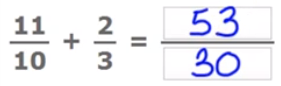
Los denominadores son 10 y 3, que son diferentes y no tienen divisores en común, por lo que tendremos que multiplicarlos entre ellos. 10 x 3 = 30, por lo que 30 será el denominador de la fracción resultante.
Para calcular el numerador, tendremos que multiplicar 11 x 3 = 33 y 10 x 2 = 20, y sumar los resultados, 33 + 20 = 53, que sería el numerador de la fracción obtenida.
El resultado final de la suma sería: 53/30
Los diversos procedimientos para realizar sumas de fracciones también pueden aplicarse a las restas, usa el que te sea más sencillo.
Fracciones Propias
En una fracción propia, el numerador es siempre menor que el denominador.
Ejemplos :
Fracciones Impropias
En una fracción impropia, el numerador siempre es mayor o igual que el denominador.
Ejemplos:
Fracciones Mixtas
Una fracción impropia también puede escribirse como un número mixto. Los números mitos contienen un número entero y una fracción propia.
Ejemplos:






0 Comentarios