Decimales
Definición de Decimales
Los números decimales se utilizan para representar números más pequeños que la unidad.
Los números decimales se escriben a la derecha de las Unidades separados por un punto. Es decir:
Centenas Decenas Unidades . Décimas Centésimas Milésimas
En la imagen que aparece a continuación, el primer cuadrado representa la Unidad. Si esta unidad la dividimos en 10 partes iguales (segundo cuadrado), representaremos las Décimas. Si las décimas las dividimos en 10 partes iguales o la unidad en 100 partes iguales (tercer cuadrado), representaremos las Centésimas.
Ejemplos de números decimales
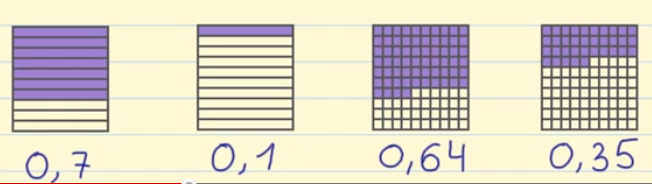
- Primer ejemplo: Si la unidad la dividimos en 10 partes iguales, tendremos décimas. Y hemos coloreado 7 de estas partes. La forma de escribirlo es 0 unidades, 7 décimas = 0,7
- Segundo ejemplo: En el segundo ejemplo también tenemos décimas y tenemos coloreadas 1. Se escribirá de la siguiente forma: 0 unidades, 1 décima = 0,1
- Tercer ejemplo: En el tercer ejemplo tenemos representadas centésimas, de las cuales tenemos coloreadas 6 décimas y 4 centésimas. Por lo tanto se escribirá: 0 unidades, 6 décimas 4 centésimas = 0,64
- Cuarto ejemplo: Tenemos centésimas (la unidad entre 100), de las cuales tenemos coloreadas 3 décimas y 5 centésimas. Lo escribiremos: 0 unidades, 3 décimas 5 centésimas = 0,35
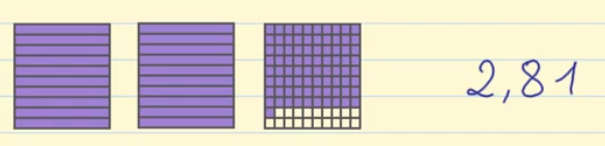
- Quinto ejemplo: Tenemos dos unidades enteras coloreadas y de la tercera unidad, que está dividida en centésimas, tenemos 8 décimas coloreadas y una centésima coloreada. Por lo tanto, se escribirá: 2 unidades, 8 décimas 1 centésimas = 2,81
¿Cual es la relación de los decimales con las fracciones?
- La Unidad se representa por 1
- La Décima es la unidad dividida en 10 partes iguales = 1/10 = 0,1
- La Centésima es la unidad dividida en 100 partes iguales = 1/100 = 0,01
- La Milésima es la unidad dividida en 1000 partes iguales = 1/1000 = 0,001
Pasar de decimal a fracción
7,508
Nos fijamos en el último número, en el 8, que ocupa el lugar de las milésimas, por lo tanto el denominador tendrá que ser 1000.
En el numerador escribiremos el número completo sin la coma:
7,508 = 7508/1000
Pasar de fracción a decimal
402/100
Como el denominador es 100, el último número del numerador (el 2) , tiene que ser las centésimas, el anterior (el 0) tienen que ser las décimas y el anterior a éste (el 4) tiene que ser las unidades, poniendo la coma detrás de las unidades.
Por lo tanto:
402/100 = 4,02
Posición de los Decimales en la Recta Numérica
Para representar un número decimal, se buscan los dos números enteros entre los que está comprendido; estos dos números determinan un segmento en la recta numérica.
El segmento se divide en 10 partes iguales (décimas), o en 100 partes iguales (centésimas), hasta llegar al número decimal dado.
Suma y Resta de Decimales
Para sumar o restar decimales se colocan los números decimales uno debajo del otro, haciendo que coincidan las unidades en la misma columna. De esta manera, también tienen que coincidir las décimas, las centésimas y el punto decimal.
Multiplicar Decimales
Para multiplicar decimales, primero multiplica como si no hubiera punto. Después cuenta el número de dígitos a la derecha del punto decimal en cada factor. Por último, coloca el número total de dígitos a la derecha del punto en el producto.
Por ejemplo, si multiplicamos 7.61✕9.2, tendremos 3 dígitos después del punto decimal en nuestro producto, pues hay 3 dígitos después de los puntos en los factores.
Dividir Decimales
El método rápido para hacer divisiones con números decimales es un truco muy fácil. Quitar el punto decimal de la división y luego volver a colocar el punto en la respuesta. Aunque pueda parecer muy complicado a primera vista, lo cierto es que con este truco seguro te será muy sencillo. Así que no esperes más y descubre cómo hacer divisiones con decimales paso a paso.
Números Racionales e Irracionales
Los números racionales son aquellos que pueden representarse como cociente de dos números enteros. Es decir, los podemos representar mediante una fracción a/b, donde a y b son números enteros y además b es distinto de cero.
El término «racional» proviene de razón, como parte de un todo (por ejemplo: «Tocamos a razón de tres por persona»).
Cada número racional se puede representar con infinitas fracciones equivalentes. Por ejemplo, el número racional 2.5 se puede representar con las siguientes fracciones:
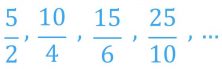
Y con todas las fracciones equivalentes a éstas.
El conjunto de todos los números racionales se representa con el siguiente símbolo:
Fíjate en que cualquier número entero es también un número racional pues puede representarse como cociente de dos números enteros.
Por ejemplo, el número 5 puede representarse con las siguientes fracciones:
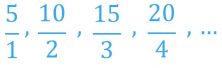
Esto quiere decir que el conjunto de los números enteros está contenido en el conjunto de los números racionales, que matemáticamente se escribe:
Para completar los números de la recta numérica, o números reales, existen números que no pueden representarse mediante el cociente de dos números enteros.
Estos números se denominan números irracionales, y los más conocidos son estos:
Los números racionales en el Antiguo Egipto
Los números racionales surgen con la necesidad de repartir una cantidad D en d partes, donde D no es necesariamente múltiplo de d.
Para calcular la cantidad que será repartida a cada parte, se necesita realizar la operación D:d, que no tiene como resultado un número entero, ya que D no es múltiplo de d.
Para dar resultado a esta operación, aparecen entonces unos números que pueden representarse de la forma D/d, distintos de los números enteros.
En el Antiguo Egipto hacían ya este tipo de repartos de «las partes de un entero», utilizando casi exclusivamente fracciones unitarias, que son las que tienen numerador 1. Es decir, las que podemos representar mediante una fracción 1/b, donde b es un número entero positivo.
Estas fracciones unitarias las representaban mediante un jeroglífico con forma de «boca abierta» que denotaba la barra de fracción, y un jeroglífico numérico escrito debajo que denotaba el denominador de la fracción.
Por ejemplo, para representar 1/4 lo hacían de la siguiente manera:
Cualquier fracción no unitaria la representaban como suma de fracciones unitarias distintas. De ahí que las sumas de fracciones unitarias se conozcan como fracciones egipcias.
0 Comentarios